Re: Translating a rotated model.
Posted by ericg on Sep 30, 2014; 11:29am
URL: https://forum.jogamp.org/Translating-a-rotated-model-tp4033250p4033255.html
EDIT: Ok, I figured out what I have to do - as always while driving .. :). After the rotate I have to translate factoring in the rotation angle.
So I will rotate, translate along vector defined by rotation x = cx + (r * cos(a)) , y = cy + (r * sin(a)) r=radius, a=angle, cxy=origin
and then translate by whatever units I am incrementing by.
The above equations are just for finding a point on an arc. They assume one of the planes is flat (ie in this case the z plane is equivalent across all vectors).
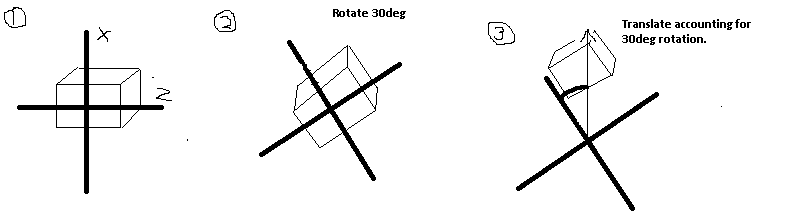
Yes I should have mentioned that I am using shaders and I am trying to avoid deprecated functions. What seems trivially simple is actually pretty difficult when I have to do the math myself. My rotate and translate functions do work but when I rotate on a fixed vertex the translate runs along a new vector (eg. if I rotate 90degrees the translate - relative to the screen - on z will run to the east west instead of north south). I need to keep the translate running north south regardless of the current rotation.
Is there an API out there that would accomplish this? That's probably what I need.
My current code:
for (float x = -30;x < 30; x+=2){
for (float z = -30; z < 30; z+=2){
{
//rotate on origin
view2 = rotate(view2,(float)rotAngle,0,1,0);
//rotate a model on its own centre. (don't want this)
/*view2 = translate(view, transX, transY, transZ);
view2 = rotate(view2,(float)rotAngle,0,1,0);
view2 = translate(view2, -transX, -transY, -transZ);*/
}
view2 = translate(view2, (float)transX - x, transY, transZ - z);
gl.glUniformMatrix4fv(iModelView, 1, false, view2, 0);
gl.glUniformMatrix4fv(iProjection, 1, false, projection, 0);
gl.glDrawArrays(GL3.GL_TRIANGLES, 0, 36); //draw 12 triangles (36 vertices).
}
}
URL: https://forum.jogamp.org/Translating-a-rotated-model-tp4033250p4033255.html
EDIT: Ok, I figured out what I have to do - as always while driving .. :). After the rotate I have to translate factoring in the rotation angle.
So I will rotate, translate along vector defined by rotation x = cx + (r * cos(a)) , y = cy + (r * sin(a)) r=radius, a=angle, cxy=origin
and then translate by whatever units I am incrementing by.
The above equations are just for finding a point on an arc. They assume one of the planes is flat (ie in this case the z plane is equivalent across all vectors).

Yes I should have mentioned that I am using shaders and I am trying to avoid deprecated functions. What seems trivially simple is actually pretty difficult when I have to do the math myself. My rotate and translate functions do work but when I rotate on a fixed vertex the translate runs along a new vector (eg. if I rotate 90degrees the translate - relative to the screen - on z will run to the east west instead of north south). I need to keep the translate running north south regardless of the current rotation.
Is there an API out there that would accomplish this? That's probably what I need.
My current code:
for (float x = -30;x < 30; x+=2){
for (float z = -30; z < 30; z+=2){
{
//rotate on origin
view2 = rotate(view2,(float)rotAngle,0,1,0);
//rotate a model on its own centre. (don't want this)
/*view2 = translate(view, transX, transY, transZ);
view2 = rotate(view2,(float)rotAngle,0,1,0);
view2 = translate(view2, -transX, -transY, -transZ);*/
}
view2 = translate(view2, (float)transX - x, transY, transZ - z);
gl.glUniformMatrix4fv(iModelView, 1, false, view2, 0);
gl.glUniformMatrix4fv(iProjection, 1, false, projection, 0);
gl.glDrawArrays(GL3.GL_TRIANGLES, 0, 36); //draw 12 triangles (36 vertices).
}
}
| Free forum by Nabble | Edit this page |